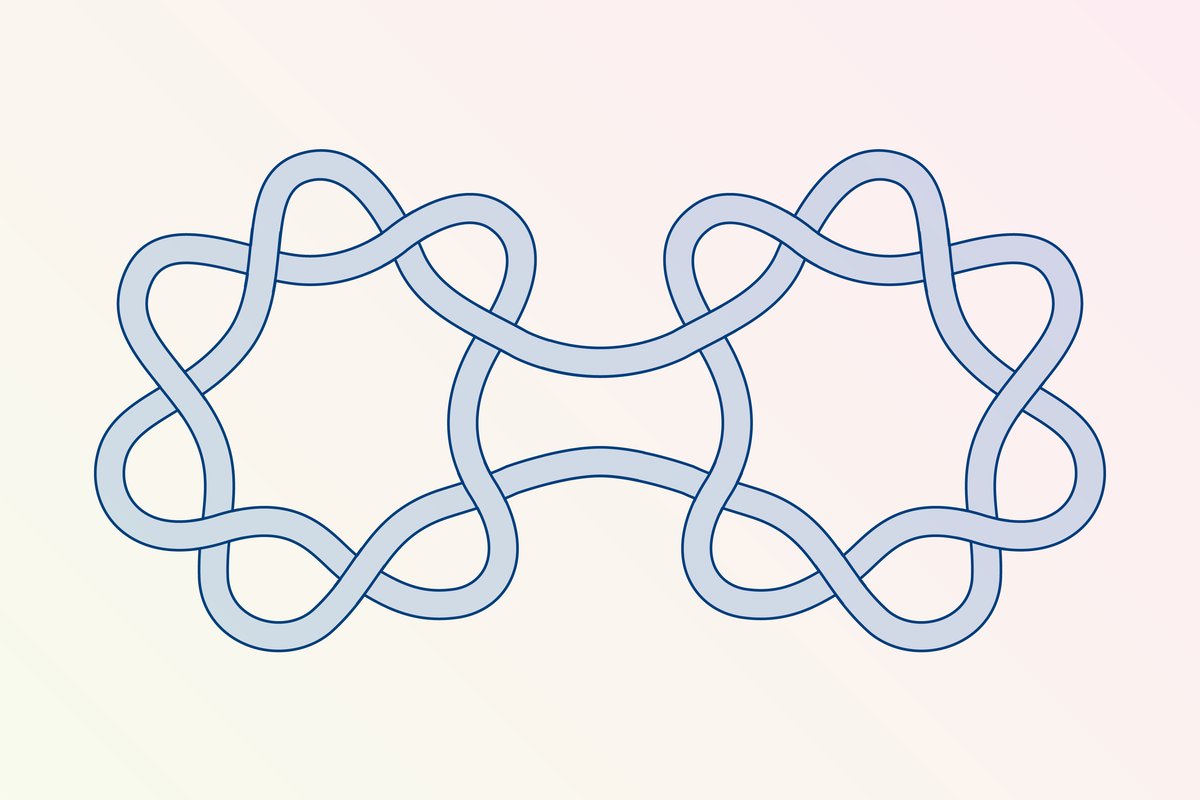
数学家们推翻了一个关于结理论的长期存在的猜想。长期以来，数学家们认为，将两个不同结的断开端连接在一起，新结的复杂度等于各个结复杂度之和。然而，研究人员最近发现了一个结，其复杂度小于其组成部分之和。这一发现挑战了我们对结复杂度的理解，并为蛋白质折叠、分子结构稳定性等领域的研究带来了新的启示。
长久以来，人们认为任何凸多面体都可以挖出一个足够大的洞，使另一个相同的物体可以穿过。这种性质被称为“鲁珀特性质”。然而，Steininger和Yurkevich近期证明了这个猜想是错误的！他们发现了一个拥有90个顶点、240条边和152个面的凸多面体，无法挖出满足条件的孔洞。他们通过计算机搜索1800万个可能的孔洞，并结合数学证明，最终证实了其结论，并将这个多面体戏称为“noperthedron”。这一发现彻底颠覆了人们对几何学的认知。
一个由Kevin Buzzard领导的国际合作项目正在使用Lean定理证明器来形式化证明费马大定理。该项目获得了英国工程和物理科学研究委员会的资助，由伦敦帝国理工学院主办。这个非标准研究项目旨在用计算机验证一个著名的数学难题的证明，其意义在于探索数学证明的形式化和自动化验证的可能性，这对于未来数学研究具有深远的影响。
本文探究了一个无限网格中数字以螺旋状排列的数学问题，该螺旋线在每次到达网格边缘时都会反向。作者通过分析螺旋线边缘和对角线上的数字规律，最终推导出一个封闭形式的表达式 (f(m, n) = (max(m, n))^2 - max(m, n) + 1 + (-1)^{max(m, n)} (m - n))，用于计算网格中任意位置 (m, n) 的数字。文章详细阐述了推导过程，包括对边缘数字和对角线数字的分析，以及如何将分段函数转化为单一的封闭形式表达式。
本文研究了方程x²+(y+zi)²=1（x, y, z为实数，i为虚数单位）的3D图像，该图像包含一个圆和一个双曲线。通过将方程分解为实部和虚部，我们可以得到两个情况：y=0时，x²-z²=1（双曲线）；z=0时，x²+y²=1（单位圆）。这个可视化方法揭示了依赖于实参数的实矩阵的复特征值的行为。文章通过两个2x2矩阵的例子，展示了如何利用该方法分析特征值，并指出这种方法可以推广到其他依赖于一个实参数的2x2矩阵。
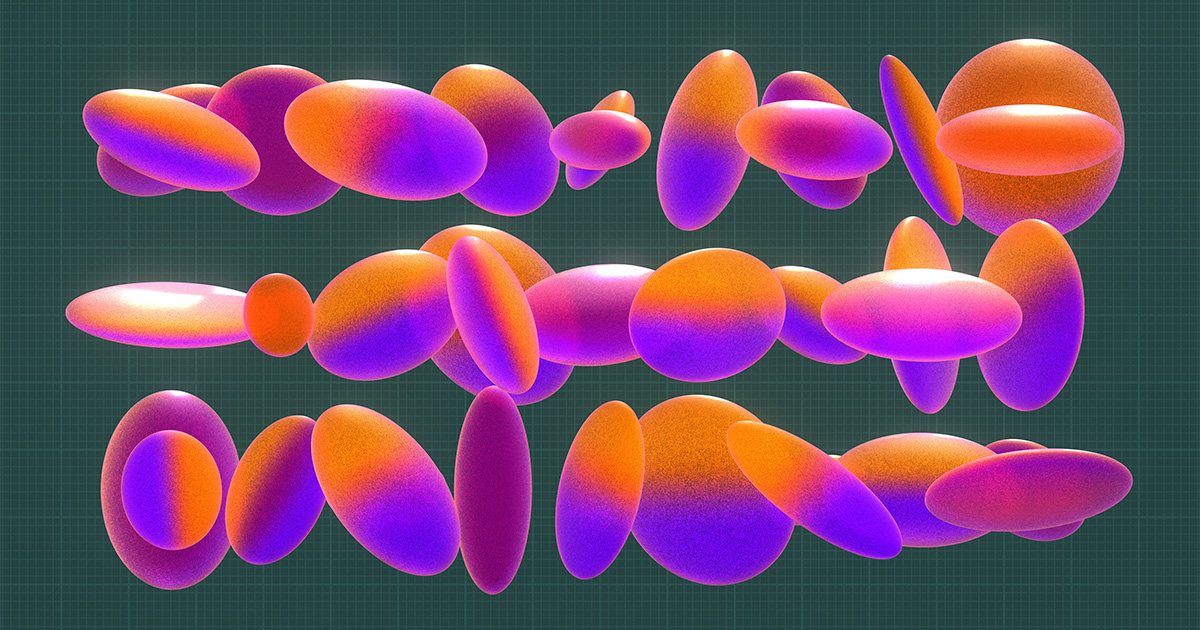
困扰数学家数十年的高维空间球体堆积问题取得了重大突破。Boaz Klartag教授另辟蹊径，运用凸几何的知识，巧妙地改进了一种已有方法，实现了球体堆积效率的显著提升。他利用随机过程调整椭球体，最终找到了比以往任何方法都更有效的球体堆积方式，其效率在高维空间中提升了数百甚至数百万倍。这一突破不仅刷新了球体堆积的记录，也重新燃起了对高维空间中球体最佳堆积方式的讨论，为密码学和通信等领域带来了新的启示。
近期，Busy Beaver 函数 BB(6) 的值得到了显著提升，从之前的 10^10^10^...^10 (15 次) 跃升至一个远超想象的数值，甚至超过了 2^^^^9。这表明 Busy Beaver 函数在 n=6 时就已超越了 ZFC 公理系统所能描述的范围，引发了对该函数未来增长趋势的重新思考，也为计算理论研究带来了新的挑战。
一群数学家在芬兰北极圈附近的一次会议上，探索了数学宇宙中无限的奥秘。他们发现了两种新的无限基数，这些基数并不符合已知的层次结构，而是“爆炸”式地产生了新的无限类别，挑战了数学宇宙的已知秩序。这一发现引发了关于数学宇宙结构的激烈辩论，有人认为它代表了实质性的进展，也有人质疑其有效性。这场争论的核心在于对数学公理体系的理解，以及对无限的本质的探索。
Tristen Harr的一篇研究论文引入并分析了一个新颖的复杂常数ΛG1，它源自黄金比例ϕ的倒数幂。作者将该常数定义为ΛG1=T+iJ，其中T=1/(2ϕ)且J=1/(2ϕ²) ，并证明它是一个大小小于1的代数数。这一性质验证了它作为多对数函数Lis(z)自变量的适用性。基于对对数(s=2)和三对数(s=3)情况的高精度数值评估，论文推测所得值Lis(ΛG1)对于所有整数s≥2都是超越数，并且不存在于域扩展Q(π,ln(2),ϕ)中。这项研究部分源于在准晶体研究中的潜在应用，其中黄金比例起着基础性作用。
几个世纪以来，素数一直吸引着数学家的注意。最近，弗吉尼亚大学的Ken Ono及其同事发现了一种全新的素数识别方法，利用整数分拆理论，他们证明了素数是无限多种特定类型的多项式方程在整数分拆函数中的解。这项发现为素数的定义提供了无限多种新的可能性，并可能激发对组合函数中隐藏的代数或分析性质的进一步研究，推动数学领域的新思考。
本文介绍了一种不同于矩阵的线性代数方法——Cracovian代数。由波兰天文学家Banachiewicz发明，Cracovian使用一种独特的乘法规则，其运算结果与矩阵乘法结果不同，且不满足交换律和结合律。虽然Cracovian在手工计算时代颇具优势，但现代计算机时代，其计算效率与矩阵乘法没有显著差异。作者通过Python代码比较了矩阵乘法和Cracovian乘法（等效于矩阵转置乘法）的计算时间，验证了这一结论。
2023年，一位退休打印技师David Smith发现了一种名为“帽子”的单块瓷砖，它能以非周期性方式平铺整个平面，引发数学界轰动。本文介绍了这一发现，并深入探讨了如何利用SAT求解器——一种鲜为人知的计算机算法——来解决有限区域的平铺问题。文章以数独游戏为例，展示了SAT求解器的应用，并进一步解释了如何利用它来找到“帽子”以及另一种名为“乌龟”的单块瓷砖的平铺方案，最终引出一种名为“幽灵”的全新单块瓷砖，它能独自以非周期性方式平铺平面，解决了困扰数学界已久的难题。文中还提供了一个在线应用，让读者可以亲身体验并探索这些奇妙的瓷砖及其平铺模式。
本文探讨了选择公理在百年数学史中的争议。从康托尔提出良序定理到策梅罗给出证明并引入选择公理，引发了数学家们激烈的讨论。文章深入分析了选择公理的不同形式，包括构造性选择公理和外延性选择公理，并指出外延性选择公理的问题在于它违反了“不能无中生有”的原则。通过在构造性类型论中进行证明，文章揭示了外延性选择公理与策梅罗选择公理以及拓扑斯理论中的选择公理之间的关系，并最终得出结论：外延性选择公理是策梅罗选择公理在构造性类型论中的正确表达。
数学家Daniel Hardisky在帕斯卡三角形中发现了π的一个新公式，这引发了数学界的广泛关注。他的发现基于Nilakantha Somayaji级数的改进，将级数中的分母与毕达哥拉斯三角形的面积联系起来，并巧妙地用组合数表示。文章还介绍了其他一些将π与帕斯卡三角形和组合数联系起来的公式，展现了π在数学领域中令人惊叹的隐藏联系。
本文探讨了科拉兹蚂蚁轨迹生成的景观相似性问题。通过分析蚂蚁轨迹的停止时间（τ）、最大欧几里得距离（α）、达到最大距离的步数（β）以及最终距离（γ），研究者发现停止时间并非景观相似性的决定性因素。最大距离（α）虽然与景观规模相关，但不足以区分不同景观。然而，达到最大距离的步数（β）似乎可以作为区分不同景观的指标，但其背后的机制仍需进一步研究。文章通过多个例子展示了β值与景观形状之间的复杂关系，并提出了一些待解之谜，例如，为什么在最大距离（α）不同时，β值有时相同，有时不同？这为科拉兹猜想的研究提供了新的视角。
一个看似简单的数学问题——无和集（sum-free set）猜想，困扰数学家数十年。该猜想探讨的是在一个整数集中，是否存在一个很大的子集，使得子集内任意两个数的和都不在该子集中。1965年，著名数学家Paul Erdős提出了这个问题，并给出了一个下界。此后，尽管许多数学家尝试改进，但进展甚微。直到今年2月，牛津大学研究生Benjamin Bedert最终解决了这个难题，证明了在任何整数集中都存在一个很大的无和子集，其大小远超之前的估计。Bedert的证明巧妙地结合了多个数学领域的技巧，为解决其他类似问题提供了新的思路。这一成果被誉为数学领域的重大突破。
作者从中学时代一个简单的几何涂鸦出发，十年后运用数学知识对其进行深入研究。这个被称为“墙上小花”的分形图案，其生成过程可以由迭代算法或L系统描述。作者发现两种方法生成的图案略有不同，并通过引入矩阵基数系统和向量数字，揭示了两种图案之间的联系，以及“约27度”旋转角的由来。进一步地，作者探索了分形的3D和4D扩展，并提出了基于四元数的新的数系。这篇文章充满了数学的巧妙和意外的发现，展现了数学之美和探索的乐趣。
作者在潜水度假时突发奇想，将Collatz猜想可视化。他巧妙地将Collatz函数的迭代过程转换为二进制分数，并绘制出相应的图形。令人惊奇的是，生成的图形展现出令人惊艳的自相似性图案，如同某种外星文字。这与2019年法国数学家Olivier Rozier的研究结果不谋而合，但两者构建方法不同。作者的简洁方法易于理解，并邀请读者探索图形中的潜在规律。
何塞·何，一位最初的诗人，因对数学的热爱而转向数学研究。他克服了本科成绩平平的劣势，在美国攻读博士学位期间，解决了困扰数学家40年的Read猜想，并最终证明了Rota猜想，这一成就为他赢得了菲尔兹奖。他的研究巧妙地将代数几何与组合数学相结合，开创了新的研究领域，展现了数学之美，也证明了“无需空间也能进行几何”的理念。
历经65年，数学家终于证明了维度126中存在一种奇异扭曲的形状，这种形状无法通过简单的“手术”方法转化为球体。这项研究揭示了高维空间中形状的奇特性质，并解决了困扰数学界多年的“末日假设”问题。研究团队利用计算机计算和理论洞见相结合的方法，完成了这项“史诗级工程”。
新南威尔士大学的荣誉教授Norman Wildberger与计算机科学家Dean Rubine合作，找到了一种求解高次多项式方程的新方法，发表于《美国数学月刊》。该方法摒弃了传统方法中使用的无理数，转而利用新型数列——“测地线”（Geode），该数列是卡塔兰数列的多维扩展。这项突破性成果解决了困扰数学家数百年的难题，并为计算机程序设计提供了新的算法改进方向。
本文探讨了这样一个问题：是否存在一个整数，其倒数的十进制表示具有一个长度恰好为10位的循环节，且该循环节包含所有十位数字（0-9）？答案是肯定的，例如72728的倒数就具有这个性质。文章进一步研究了在不同进制下具有类似性质的整数，并证明了在奇数进制下不存在这样的整数。对于偶数进制，虽然计算机搜索排除了部分进制，但该问题仍未完全解决。文章深入探讨了数论和群论的相关知识，为解决该问题提供了理论基础。
数学家们长期以来被Alon-Boppana界限所吸引，并试图构建达到此界限的图。Sarnak等人利用数论中的高深结果构建了达到该界限的“拉马努金图”。Alon和Sarnak就拉马努金图在所有正则图中所占比例打赌，引发了数学界广泛关注。多年后，Yau及其合作者通过研究随机矩阵的特征值，并巧妙地利用“宇宙猜想”，最终解决了这一难题，为这场持续多年的赌局提供了确凿的答案。
本文探讨了一个看似简单的几何问题：能否将正方形分割成任意数量的等面积三角形？答案出乎意料地复杂。1970年，Paul Monsky 证明了将正方形分割成奇数个等面积三角形是不可能的。证明巧妙地结合了斯伯纳引理和2-adic估值，通过对三角形顶点进行巧妙的染色，并利用2-adic估值分析三角形面积的2的因子个数，最终得出矛盾，证明了该命题。
本文巧妙地利用初等代数，而非微积分，重新定义了自然对数的底数e。文章通过几何直观的方式，解释了e的指数函数曲线只有一个形状，所有其他指数函数曲线都是其水平拉伸的结果。通过计算曲线在x=0处的切线斜率，文章估算出e的近似值，并进一步证明了e的指数函数的切线斜率始终等于其y值，这与微积分中的导数概念完美对应。最后，文章还通过复利极限的视角，用几何方法证明了两种定义方法的等价性，为e的定义提供了更直观、更易理解的解释。
看似简单的数独游戏，实则蕴含着深刻的数学原理。文章探讨了用图论和抽象代数两种方法解决数独问题。图论方法将数独棋盘转化为图，利用顶点染色算法寻找解；代数方法则将数独规则转化为多项式方程组，通过计算格罗布纳基找到解。两种方法都展示了数学之美，为解决数独难题提供了新思路。
两位数学家证明了长期困扰数学界的伊尔马宁多重性一猜想。该猜想关于平均曲率流中奇点的形成，此流将一般的几何物体转化为更简单、更对称的物体。通过巧妙地将曲面分解成不同区域并分析它们之间的“分离函数”，他们证明了复杂奇点不会发生，平均曲率流几乎总是导致两种简单的奇点：收缩到一点的球体或塌陷成线的圆柱体。这项突破性成果将有助于几何和拓扑学研究，并可能简化一些重要问题的证明，例如斯梅尔猜想。
本文探讨了约旦代数、八元数和李奇格之间的深层联系。文章从20世纪30年代帕斯卡·乔丹对厄米特矩阵代数性质的探索开始，引出形式上实的约旦代数及其分类，其中包含一个特殊的27维例外约旦代数。基于此，文章介绍了由约旦代数构造射影空间的方法，并重点讲解了由例外约旦代数生成的八元数射影平面。最后，文章深入探讨了一个由八元数厄米特矩阵构成的奇异时空，以及其中一个独特的积分单模格——李奇格，并指出该格在E6群作用下具有两个不同的轨道，这与通常的理解有所不同。
本文探讨了著名的Collatz猜想，以及它与密码学中ARX算法（例如ChaCha）的关联。Collatz猜想描述了一个简单的迭代函数，其最终结果是否总是收敛到1，至今仍未得到证明。文章将Collatz函数与图灵机进行类比，并指出其基于位运算的实现中，加法运算的进位传播特性导致了其难以预测的复杂性，这与ARX算法中利用加法、旋转和异或运算实现高效扩散的原理形成了有趣的对比。文章暗示，Collatz猜想的未解之谜可能与计算的固有复杂性有关，如同停机问题一样难以解决。
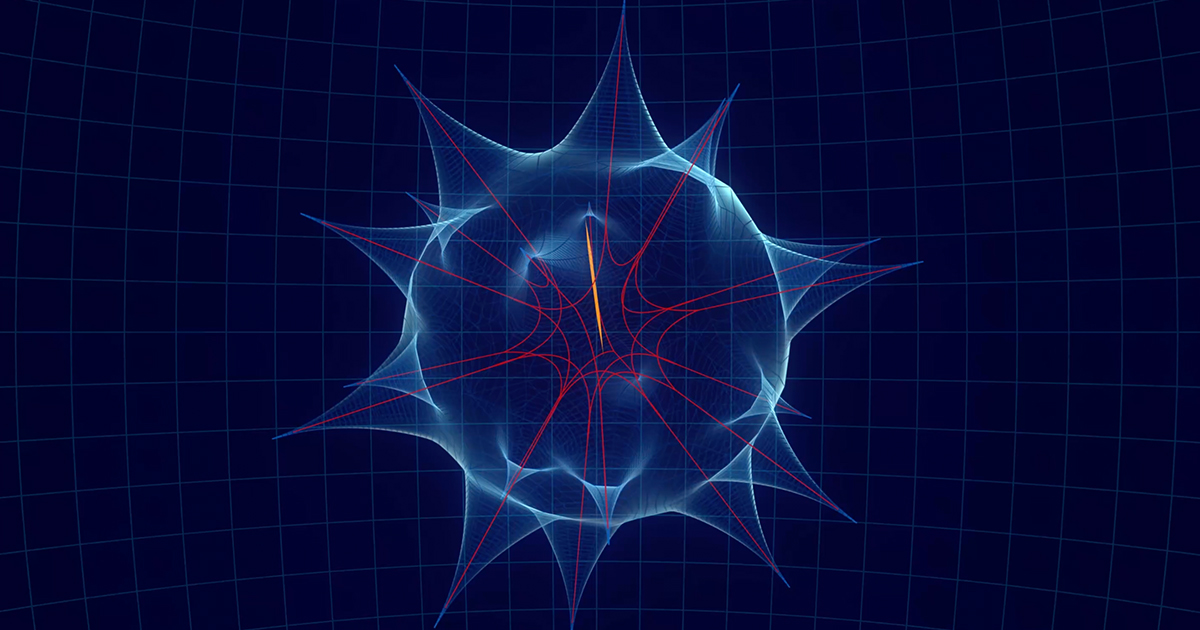
两位数学家王和扎尔证明了困扰数学家多年的三维Kakeya猜想。这个猜想与傅里叶变换密切相关，其证明如同建造一座“梦想之塔”，解决了困扰谐波分析领域的一系列难题。他们的方法类似于“永动机”，通过巧妙的计算步骤不断提高边界，最终达到了三维空间的维度。这项突破为更高维度问题的研究打开了大门，也标志着该数学领域一个时代的到来。